
Le strutture cicliche negli algoritmi
Indice degli Argomenti
- Introduzione
- Strutture cicliche indefinite
- Strutture cicliche definite o iterative
- Cicli nidificati
- Algoritmi di esempio
Introduzione
Quando all’interno di un algoritmo sorge la necessità di ripetere una sequenza di operazioni più volte, si ricorre alle strutture cicliche. Un ciclo per definizione è una sequenza di passi di un algoritmo che viene ripetuta un certo numero di volte. Il numero delle ripetizioni, è detto anche numero di iterazioni. Esistono varie strutture cicliche condizionate e iterative. Nel primo caso il numero delle iterazioni è condizionato ovvero vi è una condizione di selezione binaria che determina il numero delle iterazioni. Nella struttura ciclica iterativa vi è sempre un numero prefissato di iterazioni. In entrambe le tipologie di ciclo deve essere sempre dichiarata una variabile che svolga il controllo del ciclo ovvero su il suo valore si decide se continuare o meno il ciclo (nel caso di struttura ciclica condizionata) o come contatore delle iterazioni nel caso della struttura iterativa.
Struttura con condizione iniziale: In questo caso la condizione è inserita all’inizio del ciclo; se si verifica la stesa si passa all’esecuzione del corpo del ciclo ovvero delle istruzioni da ripetere, altrimenti si esce eseguendo la prima istruzione fuori dal ciclo.
Struttura con condizione alla fine: In questo caso la condizione è dopo il corpo del ciclo e se essa p falsa si ritorna a ripetere il corpo del ciclo, altrimenti si esce.
Nel primo caso (condizione iniziale) se la condizione non si verifica il ciclo non viene eseguito neanche una volta, mentre nel secondo caso almeno una volta il corpo del ciclo deve essere eseguito.
Strutture cicliche condizionali
La struttura generale del ciclo con condizione iniziale è:
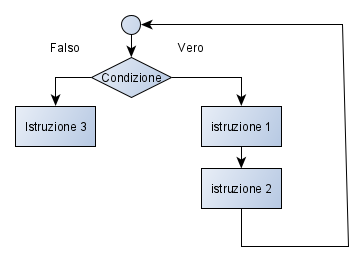
In pseudocodifce:
Mentre (condizione)
istruzione 1
istruzione 2
Fine Mentre
Istruzione 3
Puoi abbonarti al link al menù principale o cliccando sul link Abbonati Ora!