L’esercizio che si propone è il calcolo del massimo comune divisore di due numeri interi positivi a e b.
Il calcolo del M.C.D. avviene con la scomposizione dei numeri a e b in fattori primi, e il massimo comune divisore è il prodotto di tutti i fattori comuni presi con il minimo esponente.
Se i due numeri a e b sono primi inoltre il M.C.D. è pari a 1.
Alcuni esempi
a=10 e b=30 a=5*2 e 30=5*2*3 il M.C.D è quindi 5*2=10;
altro esempio:
a=96 e b=12 la scomposizione in fattori a=2*2*2*2*2*2*3 e b=2*2*3 e quindi iil M.C.D. = 2*2*3 in quanto i fattori comuni sono 2 e 3 e la potenza minima di 2 è 22.
Per individuare il M.C.D: l’algoritmo deve eseguire le divisioni di a e b per tutti i numeri interi compresi nell’intervallo [2,min(a,b)] ovvero tutti i numeri che sono compresi fino al valore minore fra a e b. Nel caso di a=96 e b=12 il numero più piccolo min(12,96) =12 e quindi i valori da utilizzare nel mio ciclo sono c=2…12. Il risultato r del M.C.D. sarà poi memorizzato in una variabile r che contiene il valore di c quando entrambi i numeri a e b sono divisibili per il valore c. Per verificare che a e b sono divisibili per c si utilizza l’operatore resto (modulo o %) della divisione intera fr adue numeri a e c e b e c contemporaneamente.
La tabella dati e:
| Uso | Nome | Tipo | Descrizione |
| input | a,b | intero | numeri in ingresso al problema positivi |
| lavoro | c | intero | contatore del ciclo per selezionare i fattori |
| output | r | intero | M.C.D. risultato |
E’ utile notare che l’algoritmo deve controllare se i due numeri in input sono positivi e solo in caso affermativo si procede all’elaborazione del calcolo M.C.D.; il calcolo può essere fatto anche con numeri negativi la generalizzazione è molto semplice una volta compreso il procedimento.
L’algoritmo risolutivo è:
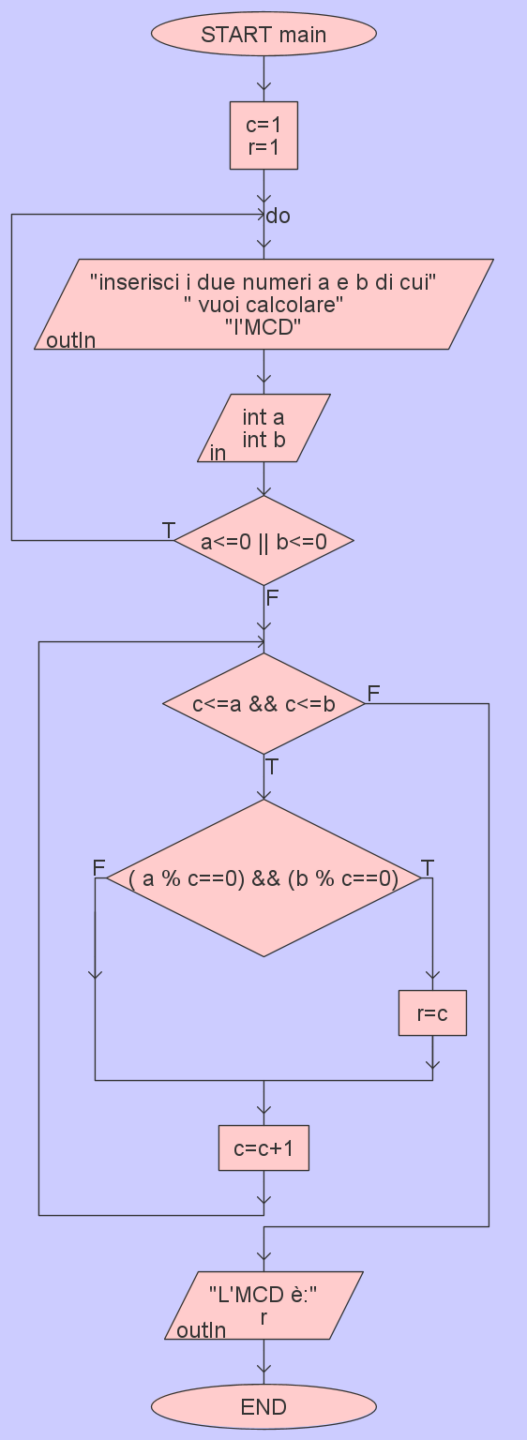
Lo pseudo – codice è:
Inizio
c←1
r←1
fai
inizio
scrivi “inserisci due numeri a e b di cui vuoi calcolare l’M.C.D.”
leggi a,b
fine
mentre ((a<=0) o (b<=0))
mentre ((c<=a) e (d<=c))
inizio
se ((a mod c=0) e (b mod c=0))
r←c
c←c+1
fine
scrivi “L’M.C.D. è:”, r
fine
L’algoritmo utilizza un ciclo pre – condizionale per calcolare il massimo comune divisore che è appunto il massimo numero che divide contemporaneamente si a che b. Per fare questo la variabile contatore c è una variabile di test in quanto partendo da 1 prova dividere a e b per c. Se entrambe le divisioni sono senza resto c è il massimo comune divisore provvisorio. Il ciclo continua fin qaundo c non uguale appunto al minio di a e b.
Il codice C++ è:
#include <iostream>
using namespace std;
int main()
{
int a,b,c,r;
c=1;
r=1;
do
{
cout << "\n Inserisici i numeri a e b di cui vuoi calcolare il M.C.D.";
cin >> a >> b;
}
while ((a<=0)||(b<=0));
while ((c<=a)&&(c<=b)){
if ((a % c==0)&&(b % c ==0))
r=c;
c++;
}
cout << "\n Il massimo comune divisore è:"<< r << endl;
return 0;
}