La rappresentazione delle informazioni nel calcolatore
Argomenti:
- La rappresentazione delle informazioni nel calcolatore
- Sistemi di numerazione posizionali
- Operazioni con i numeri binari
- Sistema di numerazione esadecimale
- Il codice ASCII e la codifica UTF-8
- Numeri interi e reali nel sistema binario
Introduzione
In questo capitolo sono esaminati i fondamenti della rappresentazione delle informazioni nel calcolatore. La rappresentazione delle informazioni nel calcolatore da sempre avviene nel sistema binario, e attraverso dei modelli di rappresentazione è possibile rappresentare qualunque informazione nel calcolatore da informazioni di carattere numerico, testuale e anche multimediali.
Esamineremo in questo breve capitolo le caratteristiche più importanti di tali modello.
La rappresentazione delle informazioni nel calcolatore
I calcolatori a livello hardware lavorano in elettronica digitale, che è caratterizzata, dall’utilizzare segnali elettrici che possono avere solo due possibili di valori, 1 passaggio di corrente, 0 nessun passaggio di corrente.
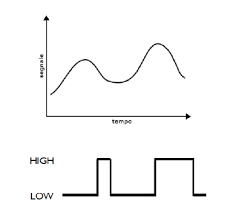
Nella figura è rappresentato un segnale analogico che varia con continuità nel tempo assumendo infiniti valori, mentre nel secondo il segnale digitale può variare solo tra due livelli prefissati denominati nella figura “High” e “Low”.
Sistema di numerazione posizionale e il sistema di numerazione binario
Grazie a quest’associazione, si definisce il bit, come cifra elementare del sistema binario, un sistema di numerazione in base 2 e posizionale. Un sistema di numerazione è definito da una base e da un insieme di cifre. Se la base è B, l’insieme delle cifre che costituiscono il sistema di numerazione è I.C.={0,1,2,3…,B-1}.
E’ altresì definito posizionale, in quanto il valore numerico della cifra dipende dalla sua posizione.
Proviamo a raffrontare con un semplice schema il sistema di numerazione decimale e quello binario:
| 102 | 101 | 100 |
| 3 | 2 | 4 |
In decimale “trecentoventiquattro”;
| 22 | 21 | 20 |
| 1 | 0 | 1 |
In decimale 4+1=5;
Da questo semplice esempio si è ottenuto che per convertire un numero binario in decimale basta scriverlo come prodotto dei singoli bit per potenze decrescenti di 2, partendo per un numero di N bit, dalla potenza 2n-1.
In formule si ha:
bn bn-1 bn-2……. b0=2n-1* bn+2n-1* bn-1+….+20* b0
Con bn sono indicate i bit, del numero binario in posizione n, n-1, n-2,…ecc. leggendo il numero binario da sinistra verso destra. Inoltre non è facile dimostrare che il massimo numero naturale rappresentabile con n bit è pari a 2n-1. Quindi se il numero è composto da 8 bit ovvero un byte il massimo intero è 28-1=255.
In informatica l’unità elementare di informazione è costituita dal byte, che come detto in precedenza è anche utilizzato come unità di misura delle capacità di memoria con i suoi multipli.
Codifica da Decimale a Binario
Per la codifica viene adoperato un metodo molto semplice basato sui seguenti passi:
- Sia N il numero decimale da convertire, si effettua la divisione per 2 del numero.
- Se il quoziente maggiore o uguale a 2 si procede ad una nuova divisione per 2 del quoziente
- Se il quoziente è già minore di 2 allora il numero binario è ottenuto assegnando come cifra più significativa l’ultimo quoziente e i rimanenti resti come cifre successive.
- Se il quoziente è già minore di 2 allora il numero binario è ottenuto assegnando come cifra più significativa l’ultimo quoziente e i rimanenti resti come cifre successive.
Supponiamo a titolo di esempio di voler trasformare il numero decimale 213 in binario, seguendo la procedura sopra descritta:
| Numero N | Base 2 |
| 213 | 2 |
| 0 | 53 |
| 1 | 26 |
| 0 | 13 |
| 1 | 6 |
| 0 | 3 |
Nella prima colonna sono visualizzati i resti in giallo, mentre nella seconda colonna in giallo è visualizzato l’ultimo quoziente. Pertanto la codifica è: 11010101(2).
Operazioni con i numeri binari
Il sistema di numerazione binario, possiede come ogni altro sistema di numerazione posizionale, le operazioni aritmetiche fondamentali somma, differenza, moltiplicazione, divisione.
Tutte le operazioni sono eseguite tenendo conto che il sistema binario lavora solo su due cifre “0” e “1”.
Riassumiamo mediante una tabella le regole per le prime tre operazioni, e in seguito analizzeremo l’operazione di divisione.
| Operazione | Regole per le operazioni | Esempi |
| Somma | 0+0=0 1+0=0 0+1=1 1+1=0 con riporto 1 | 1 1001+ 1101= 10110 Il riporto è sulla seconda cifra. La somma è svolta fra 9 e 13 in decimale e il risultato decimale è 22. |
| Differenza | 0-0=0 1-0=0 1-1=0 0-1=1 con prestito | 0 1010- 1001= 0001 Il secondo bit da destra presta un bit al bit LSB che permette di eseguire la sottrazione. E’ utile notare che la sottrazione fra numeri naturali può avvenire solo nel caso il primo numero binario è maggiore o uguale al secondo numero (sottraendo >= minuendo) |
| Prodotto | 0 x 0=0 1 x 0=0 0 x 1=0 1 x 1=1 | 1011x 11×5=55 101= 1011+ 00000+ 101100= riporto 1 su quinta cifra 110111 |
| Divisione | 1 / 1=1 0 / 1 =0 | 1011 : 101 101 10 0001 La divisione si svolge abbassando tanti bit in modo che il numero sia maggiore o uguale del divisore. SI moltiplica il quoziente che è 0 o 1 al divisore e si sottrae al dividendo. Si ripete il procedimento fin quando il divisore è maggiore o uguale del dividendo. In questo caso rimane un solo bit e quindi l’ultima cifra del quoziente è 0. Il risultato finale è quoziente pari a 10 e resto pari a 1. |
Il sistema di Numerazione Esadecimale
Come si è visto, il sistema di numerazione binario, rappresenta numeri decimali anche piccoli, con un gran numero di cifre binarie, e quindi poco si presta a rappresentare numeri molto grandi. Per ovviare a questo problema si introduce il sistema di numerazione posizionale esadecimale con base B=16 e le cui cifre sono costituite dalle cifre numeriche e dalle prime 6 lettere dell’alfabeto; quindi I.C.={0,1,2,3..,9,A,B,C,D,E,F}.
Alle lettere dell’alfabeto si attribuiscono i valori da 10 a 15.
Per codificare in esadecimale, si usa lo stesso procedimento della codifica di numero decimale in binario, con la differenza che la base che è il divisore dell’operazione è 16.
Esiste poi la possibilità di codificare dal sistema esadecimale a quello binario e viceversa, senza passare per la conversione in decimale, basta memorizzare o ricorrere alla seguente tabella:
| Numero Decimale | Numero Esadecimale | Numero Binario |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1111 |
| 15 | F |
Applichiamo, le nozioni acquisite ad un esempio convertire il numero decimale 729 in esadecimale e poi in binario senza passare di nuovo per il sistema decimale.
Applicando, la stessa procedura valida per la codifica da decimale a binario si ha:
| 729 | 16 |
| Quozienti | Resti |
| 45 | 9 |
| 2 | 13 |
A questo punto, si prende l’ultimo quoziente che è minore di 16 e e tutti resti e si scrivono le cifre anteponendo il simbolo del dollaro “$” per indicare la notazione esadecimale prendendo come cifra più significativa l’ultimo quoziente e come cifre meno significative i resti,
Quindi si ottiene:
$ 2 13 9 e quindi poiché le cifre “13” corrispondono alla lettera “D” nel sistema esadecimale e quindi otteniamo il nostro numero esadecimale $2D9:
Subito utilizzando la tabella di corrispondenza, fra i numeri esadecimali e binari otteniamo un numero binario 0010-1101-1001 i primi due zeri iniziali sono ininfluenti come nel sistema decimale e quindi il numero binario convertito è 10110110012.
Decodifica
Per convertire un numero esadecimale n decimale si utilizza la stessa formula, impostando come base 16.
Derivando la formula generale di una generica base B, si ha:
bn bn-1 bn-2……. b0=16n-1* bn+16n-1* bn-1+….+160* b0
A titolo di esempio si codifichi il numero $F3A in decimale, il numero delle cifre è 3 la cifra più significativa MSB vale come potenza 162, mentre la cifra meno significativa indicata d’ora inpoi con la sigla LSB vale 160.
Pertanto si ha:
$F3A=162*15+161*3+160*10=3840+48+10=3898.
Il Codice ASCII e la nuova codifica UTF.8
Nel paragrafo precedente, è stata definita l’unità elementare di informazione come il byte. Il byte essendo una sequenza di 8 bit, può generare 2n combinazioni differenti di 0 e 1. In questo modo è possibile attribuire ad ogni sequenza la rappresentazione di un simbolo specifico sul calcolatore come lettere minuscole e maiuscole, numeri, segni di punteggiatura, caratteri non stampabili (come il carattere spaio e a capo riga), caratteri semigrafici e altri simboli come accenti.
Tale codifica è denominata ASCII che significa “American Standard Code for Information e Interchange), che associa ad ogni sequenza un carattere. Questo codice è fortemente dipendente dalla località geografica e fin dagli albori della sua invenzione, ha generato non pochi problemi di codifica di Software e Documenti per un uso internazionale.
La tabella ASCII utilizzata nell’Europa Meridionale (codifica 850) è sotto rappresentata.
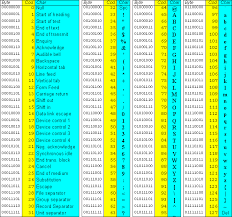
Il codice ASCII in origine era formato da sequenze di 7 bit, poi in seguito è stato esteso a 8 bit.
La lettura della tabella è estremamente semplice, si cerca il carattere del quale si vuole conoscere il corrispondente codice ASCII e si trascriva prima la coordinata di riga e poi di colonna.
Le cifre sono in formato esadecimale (oltre al simbolo “$” è possibile far seguire il numero esadecimale dal suffisso “h”), e si ottiene il codice corrispondente.
Ad esempio le cifre numeriche 0..9 corrispondono ai codici ASCII da 30h a 39h che in decimale hanno come corrispondenza i numeri decimali da 48 a 57.
Il codice ASCII, cambia come citato in precedenza, a seconda dell’area geografica di appartenenza creando non pochi problemi di conversione e localizzazione dei software e documenti del calcolatore.
Negli ultimi anni è stato introdotto il nuovo codice ASCII moderno definito UTF che utilizza per rappresentare i codici ASCII da 1 a 4 byte, mantenendo l’esatta corrispondenza fra il nuovo codice e il vecchio codice ASCII. Le più utilizzate sono a 8 bit o al limite a 16 bit denominate codifica è la UTF-8 e UTF-16. Sia nel codice UTF-8 e UTF-16 i primi 7 bit sono utilizzati per codificare il codice ASCII a 7 bit, e tutti i bit successivi per le estensioni di codifica, che consentono di raggruppare tutti insieme in modo universale i vari alfabeti delle varie aree geografiche mondiali.
Oggi tutti sistemi operativi (software di base) e software applicativi supportano questo nuovo standard di codifica.
Numeri interi, Numeri reali in binario
Nei paragrafi precedenti, è stato spiegato come rappresentare i numeri naturali in binario, tale rappresentazione non è tuttavia sufficiente, perché il mondo reale e quindi l’informatica che deve risolvere problemi deve poter utilizzare anche numeri interi e numeri reali.
La rappresentazione degli interi, nel calcolatore sono realizzate in complemento a 2, mentre i numeri reali sono rappresentati in virgola mobile. Sono due distinte rappresentazioni.
Rappresentazione dei numeri interi
Per rappresentare i numeri interi in binario si utilizza con segno il bit più a sinistra del numero binario, in una rappresentazione a 8 bit si ha:
| S | B6 | B5 | B4 | B3 | B2 | B1 | B0 |
dove con S si indica il segno e si assume che quanto il bit è posto a 1 il segno del numero binario è negativo, quando il bit è posto a zero il segno del numero binario è positivo.
Da questa costruzione, immediatamente ne deriva che l’intervallo di rappresentazione è nell’intervallo numerico (-2n-1,2n-1-1), e si osserva subito che il massimo intero positivo è minore de minimo intero negativo, in quanto nell’intervallo dei positivi occorre includere lo zero.
In una rappresentazione a 8 bit l’intervallo è (-128..8…+127).
Un’altra regola da applicare, risiede nel bloccare la rappresentazione a 8,16,32 bit. Nel caso in cui un numero binario intero sia composto da meno bit, occorre aggiungere tanti zeri a sinistra per coprire la lunghezza della rappresentazione.
A titolo di esempio il numero decimale 17, in binario è 100012, che è formato da 5 bit nella rappresentazione dei numeri interi occorre aggiungere tre zeri a sinistra 000100012 , nel quale il bit più a sinistra rappresenta il segno “+”.
Il procedimento per ottenere dal numero binario positivo il negativo si base sui seguenti passi:
- Inversione dei bit gli 0 diventano 1 e i bit 1 diventano 0;
- Al bit LSB quello più a destra per intenderci sommiamo 1;
Il risultato ottenuto è il numero binario in complemento a 2. L’operazione del passo numero 1 è definita complemento 1.
Applichiamo, il procedimento a nostro numero binario positivo 00010001;
Il numero decimale intero -17 in binario è quindi 111011112.
I numeri reali nel sistema binario e nel calcolatore
La rappresentazione dei numeri reali nel calcolatore è molto complessa, in quanto i numeri reali essi stessi sono complessi come insieme. E’ utile a tale proposito che in tale insieme sono presenti i numeri razionali e i numeri irrazionali, e i numeri trascendenti. Un numero razionale è una frazione che può esere rappresentato nella peggiore delle ipotesi con un numero periodico ad esempio la frazione 1/3 in decimale si rappresenta con , mentre ad esempio è un numero irrazionale che in decimale si approssima a 1,414 in quanto è costituito da un numero infinito di cifre dopo la virgola che non si ripetono, altrimenti si tratterebbe di un numero periodico. Esempio tipico di numero trascendente è che approssimativamente vale 3,14.
Nel sistema decimale è possibile rappresentare un qualunque numero reale con una notazione scientifica, che permette di scrivere il numero come prodotto di una parte numerica per potenze di 10.
Ad esempio il numero -11,567 in notazione scientifica si scrive come -0,11567*102, in quanto si è spostata la virgola di due posti a sinistra, invece il numero 0,0053 si può scrivere come 0,53*10-3.
Anche nel sistema binario è possibile rappresentare un numero decimale con la virgola utilizzando una notazione in virgola fissa, ovvero fissando come sempre la lunghezza della rappresentazione che per i numeri reali (e quindi decimali che sono in inclusi nell’insieme R), a 32 bit o 64 bit, i primi in singola precisione e i secondi a doppia precisione.
A titolo semplificativo immaginiamo di rappresentare un numero binario con la virgola a 16 bit fissando per la parte intera 10 cifre e per la parte frazionaria 6 bit.
In formule si:
a9a8a7a6a5a4a3a2a1a0,b5b4b3b2b1b0 (1)
In sintesi le cifre dopo la virgola si convertono come prodotto delle cifre binarie per potenze decrescenti negative di 2 da sinistra verso destra.
Ad esempio il numero binario 10101,011012
si converte in 1*24+1*22+1*20,1*2-2+1*2-3+1*2-5=(21),(1/4+1/8+1/32)=11,40625.
Nel calcolatore come per i numero in base 10 si usa la notazione scientifica è possibile utilizzare la notazione normalizzata che scompone il numero come prodotto di una parte frazionaria per una potenza di 2, indicando anche il segno del numero.
In formule:
N,D=(-1)s*(mantissa*2esponente
N rappresenta la parte intera del numero con segno e D la parte frazionaria, mentre la mantissa è un numero compreso fra zero e uno. Ad esempio nel sistema decimale la notazione normalizzata del numero 3,97 è 0,397*101.
Analogamente nel sistema binario il numero, può essere rappresentato in notazione normalizzata come nella formula (1) con alcune modifiche a0,bnbn-1bn-2…….b0 (1.2). La cifra a0 rappresenta la parte intera del numero binario scritto in notazione normalizzata.
In realtà le cose nel calcolatore sono un attimo più complesse perché i numeri reali sono rappresentati in singola e doppia precisione secondo la notazione IEEE754 introdotta nel 1985, che prevede i numeri in virgola mobile in 32 bit o 64 bit.
Lo schema di un numero binario in virgola mobile a 32 bit per essere più semplici è quello sttoriportato:
| Segno bit 1 numero negativo bit 0 numero positivo | Caratteristica rappresenta l’esponente della potenza di 2 della (1) in binario aggiungendo all’esponente +127 se l’esponente è diverso da zero, altrimenti si aggiunge 126 La caratteristica è pari a 8 bit | Mantissa rappresenta la parte frazionaria con lunghezza massima di 23 bit |
Chiariamo da subito, che la caratteristica si calcola aggiungendo prima in decimale all’esponente il numero +127 e poi convertendolo in binario se l’esponente è diverso da zero, +126 se l’esponente è pari a zero.
Proviamo a questo punto con un esempio a convertire un numero reale 34,759; per effettuare la conversione occorre chiarire il procedimento.
Fissata il numero dei bit della mantissa M, si moltiplica la parte frazionaria per 2, il risultato è un numero maggiore di 1 e minore di 2, oppure minore di 1 e maggiore o uguale a 0. Nel primo caso il bit da riportare nella mantissa da destra verso sinistra è 1, nell’altro caso 0. Al risultato se superiore a 1 si sottrae 1, altrimenti rimane invariato. Il risultato si moltiplica per 2 e si itera il procedimento tante volte quanti sono i bit della mantissa da ottenere. La parte intera si converte con la rappresentazione degli interi in complemento a 2, alla fine si normalizza il numero per determinare la caratteristica, come spiegato nella tabella sopra.
Vediamo, come convertire il numero ipotizzando una notazione semplificata che preveda 16 bit totali di cui 8 per la mantissa M (abbiamo già detto che la notazione IEEE754 prevede delle lunghezze di 32 o 64 bit totali).
In base a questo ragionamento la parte intera 34 in binario è 0001000102 , mentre per la parte frazionaria applichiamo il procedimento esporto:
0,759*2=1,518 bit 1
1,518-1=0,518*2=1,036 bit 1
1,036-1=0,036*2=0,072 bit 0
0,072*2=0,144 bit 0
0,144*2=0,288 bit 0
0,288*2=0,576 bit 0
0,576*2=1,152 bit 1
1,152-1=0,152*2 bit 0
Il procedimento termina perché sono stati utilizzati tutti i bit della mantissa, ora il nostro numero binario è quindi (la mantissa è in rosso):
00100010,110000102 il primo bit è il segno portandolo in notazione normalizzata si ha:
0,010001011000010*27 quindi risulta che la lunghezza della mantissa per questo livello di approssimazione ovvero 8 bit per la parte frazionaria occorrono un numero maggiore di bit.
Utilizziamo allora proprio la notazione in singola precisione IEEE754 che prevede 23 bit per la mantissa, 8 per la caratteristica e 1 per il segno.
La caratteristica è +7 aggiungiamo 127 otteniamo 134 come caratteristica in eccesso 127, che convertita in binario è 100001102 in definitiva il numero è: 010000110-010001011000100000000002.
Alla fine della mantissa che è quella in rosso, si sono aggiunti gli 0 mancanti per completare la rappresentazione.